Conexionismo - Modelos conexionistas de redes neuronales

VIII.1. Redes de McCulloch-Pitts o redes de neuronas formales

VIII.3. EL PANDEMONIUM: UN MODELO PARA EL RECONOCIMIENTO DE PATRONES

VIII.3.1. La tarea de reconocimiento de patrones: dos explicaciones, el modelo de plantillas y el modelo de análisis de características

VIII.3.2. El Pandemonium: rasgos principales

VIII.3.3. El Pandemonium: base experimental

VIII.3.4. El Pandemonium: dificultades

VIII.3.5. El Pandemonium y el conexionismo

VIII.4. NETtalk: aprender a leer en inglés

VIII. 1. REDES DE McCULLOCH-PITTS o redes de neuronas formales

En 1943, Warren McCulloch (neurofisiólogo) y Walter Pitts (matemático) publicaron en el Bulletin of Mathematical Biophysics "Un cálculo lógico de las ideas inmanentes en la actividad nerviosa"; en este artículo defendieron la tesis de que las actividades de las neuronas y las relaciones existentes entre ellas podían estudiarse mediante la lógica proposicional. Creyeron que las neuronas tenían un comportamiento biestable (al producir salidas todo-nada) y que, en este sentido, eran semejantes al comportamiento también biestático de los conmutadores eléctricos (abierto-cerrado). Junto con la idea relativa al comportamiento supuestamente lógico de las neuronas, presentaron también la idea de construir máquinas de computar con una arquitectura similar a las neuronas. A pesar de su conocimiento insuficiente de las neuronas y las sinapsis orgánicas, sus ideas han tenido mucha importancia en el desarrollo de la psicología cognitiva: consideraron que las leyes que gobiernan la mente tienen más que ver con las leyes que gobiernan la información que con las relativas a la materia (idea más común a la psicología cognitiva clásica que al conexionismo); pero en su comprensión del aprendizaje anticiparon también ideas conexionistas: dieron más importancia al aprendizaje que a factores innatos, consideraron que nuestro cerebro comienza con redes aleatorias, que los estímulos provocan conexiones de una determinada manera y que los estímulos posteriores, si son fuertes y constantes, llevarían a la red a manifestar una configuración determinada. Esta configuración determinaría que la respuesta de la red fuese distinta ante nuevos estímulos. En definitiva, su artículo fue importante al tratar al cerebro como un organismo computacional.

Demostraron también que redes neuronales sencillas, conectadas entre sí mediante sinapsis excitadoras o excitadoras e inhibidoras, y asignando un valor umbral para la activación de la unidad de salida, eran capaces de representar adecuadamente las leyes lógicas fundamentales. Llamaron neuronas “formales” a las neuronas que componen dichas redes. Aunque intentaron modelar aspectos elementales de las neuronas biológicas, las neuronas McCulloch-Pitts no eran otra cosa que conmutadores lógicos, semejantes a los circuitos lógicos que se pueden crear mediante simples interruptores por los que pueden fluir la corriente eléctrica.

Las redes siguientes son algunos ejemplos que presentaron en su artículo, y, como se indica, sirven para calcular los valores de verdad de la disyunción, la conjunción y la conjunción con negación. Las neurona podía recibir tanto entradas excitadoras como inhibidoras. La neurona tomaba valor 0 cuando estaba desactivada y valor 1 cuando estaba activada (es decir utilizaba una función de activación tipo umbral). La salida de la unidad era 1 cuando estaba activada y 0 cuando estaba desactivada (por lo tanto la función de transferencia era la función identidad). En todos los casos el peso sináptico de las conexiones excitadoras era 1. Las sinapsis inhibidoras provocaban la inhibición total de la neurona: independientemente de la cantidad de excitación que le llegase desde las sinapsis excitadoras, si una sinapsis inhibidora se excitaba, la neurona quedaba totalmente desactivada y producía la salida 0; por lo tanto, la neurona producía 1 de salida si y sólo si no recibía ninguna señal inhibidora y las señales excitadoras que recibía igualaban o superaban el valor umbral. Esta es una de las diferencias fundamentales respecto de las redes que se utilizan actualmente

pero también podemos utilizar los siguientes gráficos para representar las neuronas McCulloch- Pitts, gráficos que seguramente resultan más intuitivos (tomado de Estructura, dinámica y aplicaciones de las redes de neuronas artificiales, VVAA, Editorial Centro de Estudios Ramón Areces, p. 103); el número en el interior de la neurona indica el umbral

Volver al índice

VIII. 2. PERCEPTRONES

En 1958 Frank Rosenblatt escribió The Perceptron, a Probabilistc Model for Information Storage and Organization in the Brain. Rosenblatt rechazó el uso que McCulloch y Pitts hicieron de la lógica simbólica aplicada a las redes y defendió métodos probabilísticos. En esta obra llamó “perceptrones” a unas redes McCulloch-Pitts capaces de modificar los pesos de sus conexiones si las respuestas de la red no eran las correctas y demostró que estas redes se podían entrenar para clasificar ciertos patrones en iguales o distintos, por tanto que eran capaces del reconocimiento de formas sencillas.

Ejemplo de un Perceptrón sencillo
las unidades y conexiones que se muestran son sólo ilustrativas
y no reflejan totalmente la complejidad del modelo

El mecanismo de procesamiento del Perceptrón es el siguiente: el patrón a reconocer incide en la capa sensorial; cada una de las unidades sensoriales responde en forma todo o nada al patrón de entrada; las señales generadas por las unidades sensoriales se transmiten a las unidades de asociación; éstas unidades se activan si la suma de sus entradas sobrepasa algún valor umbral. Cuando una unidad de la capa asociativa se activa, provoca una señal de salida, la cual va por las sinapsis correspondientes hasta las unidades de la capa de salida; estas responden de forma muy similar a las de las unidades de asociación: si la suma de sus entradas sobrepasa un umbral, producen un valor de salida 1, en caso contrario su salida vale 0 (por lo tanto, la función de actividad de las unidades era tipo umbral, produciendo actividades con valores discretos, 0 y 1, y la función de trasferencia era la función de identidad).

La representación del Perceptrón utilizada más arriba puede inducir a pensar que se trata de una red multicapa, pero este no es el caso: las conexiones entre las unidades sensitivas y las de la capa de asociación son fijas, no se modifican durante el aprendizaje; siempre es preciso presentar a la red el patrón de entrada, y esto se puede hacer de varias formas, por ejemplo el usuario puede introducir los datos en el ordenador mediante el teclado, pero si la red está conectada a algún sensor (como el Perceptrón intentaba simular) los datos le llegarán a través de él. Por lo tanto, a todos los efectos el Perceptrón puede considerarse como una red de dos capas, sin unidades ocultas.

El Perceptrón era una red capaz de aprendizaje. En su configuración inicial a los pesos de las conexiones se les da valores arbitrarios, por lo que ante la presencia de estímulos la red genera respuestas arbitrarias, respuestas que no coinciden con las deseadas. Se considera que la red ha conseguido aprender cuando los pesos se han ajustado de tal modo que la respuesta que emite es la deseada. El procedimiento propuesto por Rosenblatt para este entrenamiento era sencillo: se le presenta a la red un patrón cuya señal se transmite hasta la capa de salida, provocando la activación de alguna de sus unidades; si se activan las unidades de respuesta correcta, no se hace ningún ajuste de sus pesos; si la respuesta es incorrecta se procede de la manera siguiente: si la unidad debía estar activada y no lo está, aumentar todos los pesos de sus conexiones; si la unidad debía estar desactivada y está activada, disminuir los pesos de sus conexiones. Se repite este procedimiento con todos los patrones deseados de estímulo-respuesta. Rosenblatt creyó que era posible hacer que los pesos converjan en un conjunto de valores, a partir de los cuales le es posible a la red computar cada uno de los patrones de entrada para producir los correspondientes patrones de salida.

En el párrafo anterior se ha descrito de modo cualitativo y poco preciso la modificación que han de sufrir los pesos cuando la red produce errores; existen varios algoritmos que se pueden utilizar para detallar con exactitud el modo de modificar los pesos de las conexiones, por ejemplo:

si la respuesta es 0 debiendo ser 1, wij (t+1) = wij(t) + µ*oi;
si la respuesta es 1 debiendo ser 0, wij (t+1) = wij(t) – µ*oi

donde
wij : es el peso correspondiente a la conexión de la unidad i con la unidad j
oi : es la salida de la unidad i
µ : es la tasa de aprendizaje que controla la velocidad de adaptación

En 1969 Marvin Minsky y Seymour Papert escribieron Perceptrons: An Introduction to Computational Geometry. En esta obra analizaron las capacidades y limitaciones del Perceptrón, y demostraron que hay ciertas clases de problemas que el Perceptrón y cualquier modelo simple de dos capas no puede resolver. Los perceptrones sólo pueden distinguir tramas o patrones linealmente separables, y dado que hay muchos e importantes problemas que no son linealmente separables, concluyeron que los perceptrones son poco adecuados como clasificadores de patrones. Además ampliaron su crítica afirmando que esta dificultad no se puede resolver con redes multicapa (algo que posteriormente se demostró erróneo). Decimos que un patrón o conjunto de datos de entrada de la red es linealmente separable cuando el espacio de todas las entradas puede dividirse en dos regiones, quedando en uno de los lados del hiperplano las correspondientes a una categoría y en la otra parte del hiperplano las correspondientes a otra categoría. Se llaman hiperespacios a los espacios n-dimensionales (por ejemplo, el espacio euclideo es un caso particular de hiperespacio, y consta de tres dimensiones); se llaman hiperplanos a los objetos de n-1 dimensiones que dividen un hiperespacio de n dimensiones en varias regiones; en el caso de un espacio bidimensional, el hiperplano es una línea que descompone el espacio en dos regiones; en el caso del espacio tridimensional, el hiperespacio es un plano y puede dividir el espacio en tres regiones. En la resolución de problemas puede ser útil la referencia a los hiperplanos puesto que permiten separar regiones de puntos de un hiperespacio en categorías individuales o clases, por lo que es un recurso útil para distinguir unas clases de otras.

La obra de Minsky y Papert supuso un importante freno en el desarrollo de la investigación en redes neuronales pues convenció a la administración americana de la bondad de la arquitectura tradicional (la arquitectura Von Neumann) y de la incompetencia de las arquitecturas de redes neuronales, y llevó a muchos investigadores a preocuparse por la línea tradicional en psicología cognitiva e Inteligencia Artificial y despreocuparse de los modelos conexionistas.

Se puede comprender la crítica de Minsky y Papert y el problema de la separabilidad lineal si nos fijamos en uno de los más conocidos y sencillos problemas que la red no puede resolver: el relativo al problema XOR o disyunción exclusiva. Dado que el Perceptrón es capaz de asociar patrones de entrada con patrones de salida y que las tablas de verdad de los funtores son también correspondencias entre pares de valores de verdad y el valor del enunciado molecular compuesto por el funtor correspondiente, parece que podemos utilizar los perceptrones para decidir los valores de verdad de los enunciados moleculares; por ejemplo, la tabla de verdad de la función AND (la conjunción) y de la función OR (la disyunción inclusiva) son las siguientes

x1	x2	x1∧ x2	x1	x2	x1∨ x2
0	0	0	0	0	0
0	1	0	0	1	1
1	0	0	1	0	1
1	1	1	1	1	1

tabla de verdad de la conjunción

tabla de verdad de la disyunción inclusiva

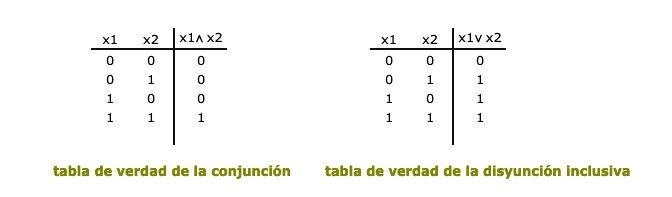
La tarea que tiene que realizar el Perceptrón es, en el primer caso, aprender a asociar la entrada (1,1) con la salida 1, y las entradas restantes con la salida 0; en el segundo caso debe aprender a asociar la entrada (0,0) con la salida 1, y las entradas restantes con la salida 1. La red que se ha de utilizar para realizar la computación debe constar de dos unidades de entrada y una unidad de salida: cada unidad de entrada recoge uno de los elementos del patrón de entrada y la unidad de salida produce una salida, que es la que corresponde a la solución.

Como se ha indicado, para la función OR (disyunción inclusiva) la red debe ser capaz de devolver la salida 0 si se le presenta el patrón (0,0) y para los restantes patrones la salida 1; para la función AND (la conjunción) la red debe devolver la salida 1 para el patrón (1,1) y 0 para los restantes patrones. Veamos el caso de la función OR:

x1 y x2 son las entradas a la neurona;
en las neuronas de la capa de entrada la salida es igual a su entrada;
w1 y w2 son los pesos de las conexiones entre las neuronas de entrada y la neurona de salida;
la entrada neta es la suma ponderada de las entradas (w1x1 + w2x2);
la función de activación de la neurona de salida es la función identidad;
la salida es discreta tomando alguno de los valores del par (1,0);
la función de salida o transferencia es de tipo escalón, es decir establece un umbral que es necesario superar para que la salida sea 1.

De este modo, tendríamos:

entrada neta = w1x1 + w2x2

activación de la unidad de entrada = w1x1 + w2x2

valor de salida = 1 si w1x1 + w2x2 ³ umbral
0 si w1x1 + w2x2 < umbral

Para el caso de la disyunción inclusiva, el umbral puede ser cero o superior, sin embargo, para la conjunción el umbral ha de ser mayor que cero. Es posible entrenar a la red para que modifique sus pesos de modo que converjan en los adecuados para producir el patrón de salida adecuado. Expresado en términos de hiperplanos, la red resuelve los problemas lógicos anteriores si existe un hiperplano capaz de distribuir el plano en dos regiones: en el caso de la función AND (la conjunción), en una región quedarían los patrones de entrada (0,0), (0,1), (1,0) y en la otra región el patrón (1,1); en el caso de la función OR (la disyunción inclusiva), en una región quedaría el patrón (0,0) y en la otra los patrones de entrada (0,1), (1,0), (1,1); estos patrones corresponden a los valores de verdad posibles de los enunciados que componen el enunciado molecular. Veamos cómo se puede utilizar este método:

primero construimos un plano en el que se pueda representar cada uno de los vectores de entrada; el plano tendrá las coordinadas x1, x2;
en segundo lugar, mediante puntos, situamos en el plano los cuatro valores de verdad correspondientes a la función lógica que se quiere computar;
en tercer lugar, representamos en el plano la ecuación w1x1 + w2x2 (que corresponde a la función de activación); w1 y w2 son los pesos y x1 y x2 los distintos patrones de entrada. Esta ecuación es la ecuación de una línea en el plano x1, x2.

La recta divide el espacio en dos regiones que podríamos interpretar uno como correspondiendo al valor 1, y el otro como correspondiendo al valor 0; si en cada una de estas regiones se incluye el patrón de entrada correspondiente, entonces podemos decir que la red es capaz de computar la función lógica, pues distribuye adecuadamente los valores de verdad del patrón de entrada con el valor de salida que les debe corresponder. En las figuras siguientes se muestra el plano xi, x2 con los cuatro puntos que corresponden a los cuatro vectores de entrada (0,0), (0,1), (1,0), (1,1).

	en la función AND al vector (0,0) le debe corresponder la salida 0, al (0,1) la salida 0, al (1,0) la salida 0 y al (1,1) la salida 1 (en el gráfico la salida se pone en negrita); como se puede apreciar, la recta generada por la ecuación w1x1 + w2x2 permite distribuir correctamente los valores de salida, luego la red podría computar la función lógica AND
	en la función OR al vector (0,0) le debe corresponder la salida 0, al (0,1) la salida 1, al (1,0) la salida 1 y al (1,1) la salida 1; como en el caso anterior, la recta también distribuye correctamente los valores de salida, por ello la red podría computar la función lógica OR

Sin embargo, la red de dos capas no puede computar adecuadamente la función lógica XOR (la disyunción exclusiva); veámoslo:

x1	x2	x1 >¾< x2
0	0	0
0	1	1
1	0	1
1	1	0

tabla de verdad de la disyunción exclusiva

si ahora representamos en el plano las vectores de entrada y los valores de verdad correspondiente, tenemos

Se observa fácilmente que con una sola línea es imposible separar los puntos 1 y 1 de los puntos 0 y 0; no hay forma de disponer la línea de modo que separe los conjuntos de puntos citados. Esto es precisamente lo que se quiere indicar cuando se dice que este problema no es linealmente separable. Si tuviésemos dos líneas entonces sería posible descomponer el espacio en tres regiones, en dos de las cuales se encontrarían los puntos 0 y en la otra los puntos 1. Los perceptrones de dos capas no pueden dar lugar más que a una línea, pero podemos conseguir dos líneas si entre la capa de entrada y la de salida situamos una capa intermedia con dos neuronas, cada una de las cuales nos permitirá obtener una línea (ver gráficos de la página siguiente). En la época de Rosenblatt no se disponía de un algoritmo de aprendizaje adecuado para redes con capas ocultas y hubo que esperar a los años ochenta para su perfecto desarrollo (la regla delta generalizada) y, por lo tanto, para la superación del problema de la separabilidad lineal.

Red multicapa con unidades ocultas que resuelve correctamente el problema XOR. Si el umbral de la unidad c = 0.4, de la d = 1.2, de la e = 0.5 y los pesos wca = 1, wcb = 1, wda = 1, wdb = 1, wec = 0.6, wed = -0.4, la red da lugar a la representación gráfica inferior. Se aprecia que las dos líneas crean una región en donde se sitúa el conjunto formado por 1 y 1 y dos regiones en donde se sitúan los otros dos valores; por lo tanto, la red resuelve el problema XOR

Volver al índice

VIII. 3. el Pandemonium: un modelo para el reconocimiento de patrones

VIII. 3. 1. La tarea de reconocimiento de patrones: dos explicaciones, el modelo de plantillas y el modelo de análisis de características

Una característica del sistema de procesamiento visual humano es su flexibilidad: somos capaces de identificar un patrón, un tipo de estímulo, con independencia sus posibles variaciones en tamaño, posición en el contexto y orientación espacial; e incluso cuando su forma varía en ciertos límites; fijémonos en los siguientes ejemplos:

En todos ellos reconocemos sin dificultad la letra "E", y todos ellos pueden interpretarse como variaciones del mismo patrón, el correspondiente a dicha letra. Podemos llamar “reconocimiento de patrones” al hecho de identificar distintos estímulos como perteneciendo a la misma clase, como siendo del mismo tipo. Los psicólogos han presentado diversas teorías para comprender el modo en que nuestra mente es capaz de reconocer patrones; una de las primeras y más sencillas es la de “comparación de plantillas”. Según esta teoría en nuestra memoria debe haber un modelo o plantilla correspondiente a cada forma que podamos reconocer. Cuando vemos un objeto, la imagen que se produce en la retina se la compara con las plantillas almacenadas en nuestra memoria y aquella que mejor se ajusta a la imagen retiniana es la que identifica al objeto visto. Fácilmente se ve que esta teoría no es satisfactoria: un cambio en la posición, tamaño u orientación del objeto provocaría un desajuste que haría imposible el reconocimiento. Además no podríamos reconocer formas deterioradas pues tampoco coincidirían con las plantillas.

Podríamos modificar la teoría para superar estas dificultades: por ejemplo suponiendo que existen tantas plantillas almacenadas como variedades posibles de posición, rotación, tamaño y distorsión, pero está claro que ésta no es una buena solución pues exigiría un número tan grande de plantillas que ni siquiera el cerebro podría almacenar. Otra estrategia más razonable consistiría en suponer que antes de la comparación del input retiniano con las plantillas nuestra mente realiza un análisis preparatorio, lo que algunos autores llaman “preprocesamiento”: mediante este análisis las imágenes retinianas se someten a un proceso de normalización que los traduce a un formato estándar compatible con los formatos de las plantillas existentes en nuestra memoria (ajustando el tamaño y la orientación por ejemplo). Existen algunos resultados experimentales que parecen avalar la hipótesis de la normalización.

Algunas de las dificultades del modelo de plantillas se pueden resolver con otro modelo algo más complejo que el anterior: el modelo basado en el análisis de características. Esta teoría defiende que nuestra mente no trabaja con copias exactas de la información sino con el análisis de las características internas de cada patrón; por ejemplo, el sistema visual utilizaría un análisis de características al menos en las siguientes dimensiones: líneas y sus variantes (verticales, horizontales, oblicuas), ángulos y sus variantes y curvas. En la memoria se representa cada patrón mediante una lista de sus características geométricas y (al menos en las versiones más elaboradas) sus correspondientes pesos. Así, la letra "A" podría representarse mediante la siguiente lista de características: pesos altos: dos líneas inclinadas, una hacia la derecha y otra hacia la izquierda, una línea horizontal, un ángulo apuntando hacia arriba; pesos bajos o nulos: líneas verticales, líneas curvas discontinuas, ángulos rectos, etc. El patrón estimular activa los detectores de características, y la configuración de la activación resultante se compararía con la de los patrones almacenados en la memoria; la configuración que mejor se ajuste determinaría la interpretación perceptual del sistema.

VIII. 3. 2. El Pandemonium: rasgos principales

El Pandemonium propuesto por O. Selfridge en su escrito de 1959 Pandemonium: A paradigm for learning es precisamente uno de los primeros y más conocidos modelos de reconocimiento de patrones basados en el análisis de características. Originariamente el Pandemonium se concibió como un programa de ordenador para reconocer señales del código Morse, pero posteriormente se le dio una interpretación psicológica como modelo de reconocimiento alfanumérico. La exposición y comentarios que siguen se refiere precisamente a la versión más conocida del Pandemonium (la de Lindsay y Norman en su obra Introducción a la psicología cognitiva) y cuyo objetivo es el reconocimiento de letras. El Pandemonium consiste en varios conjuntos de unidades a las que Selfrigde dio el nombre de “demonios”, unidades que realizan distintas tareas y provocan la información de salida (la identificación de la forma presentada al sistema). El dibujo siguiente es una representación habitual del Pandemonium (tomado de Linsay y Norman, Introducción a la psicología cognitiva).

Los tipos de demonios de los que consta el modelo son los siguientes:

Demonios de la imagen: su tarea es registrar la imagen del signo externo.

Demonios de características: la tarea de las unidades de este tipo es analizar la imagen registrada; cada demonio de características está especializado en un aspecto particular de la forma (unos detectan líneas, otros ángulos, otros curvas, ...) por lo que el procesa- miento en este nivel consiste en la descomposición de la forma en sus características relevantes; cada demonio de características detecta la presencia de alguno de los rasgos para los que ha sido definido (por ejemplo el demonio correspondiente a las líneas verticales detecta la presencia y número de líneas verticales en la figura).

Demonios cognitivos: reciben y examinan la información de los demonios de características; cada demonio cognitivo está especializado en el reconocimiento de una forma (por ejemplo, uno para la letra "A" otro para la "B", ...) y busca en los datos que les ofrecen los demonios de características la presencia de los rasgos que definen la letra en la están especializados (por ejemplo el demonio cognitivo de la letra "A" buscará la presencia de una línea horizontal, dos oblicuas y tres ángulos agudos).

Demonio de decisión: cuando un demonio cognitivo encuentran una característica que buscaba empieza a gritar y cuantas más características descubre más grita; la tarea del demonio de decisión es escuchar el Pandemonium producido por los demonios cognitivos y seleccionar el que grita más fuerte; la interpretación que el sistema hace de la forma que se le presenta corresponde a la letra decidida por este demonio.

Una cuestión muy importante que tiene que decidir el diseñador de un Pandemonium es la de determinar las características de cada patrón. Se han dado distintas propuestas de los criterios más adecuados para ello, propuestas entre las que destaca la que presentó en 1969 E. J. Gibson en su obra Principles of perceptual learning and development. Los criterios que defendió se referían a la selección de la lista de características para las letras mayúsculas, y son los siguientes:

1. Las características críticas deben estar presentes en algunos miembros, pero no en otros, de modo que permitan una clara distinción entre ellos.

2. No deben variar cuando cambia el brillo, tamaño o perspectiva.

3. Deben producir un único patrón para cada letra.

4. La lista no debe ser muy extensa.

Más explícita es la propuesta de Linsay y Norman en su libro ya clásico Introducción a la psicología cognitiva. El cuadro siguiente (tomado de dicha obra) presenta los demonios de características necesarios para la identificación de una letra y los valores que activan para cada una de las letras del alfabeto. Mediante las siete características citadas podemos identificar adecuadamente la totalidad de las letras.

	Líneas verticales	Líneas horizontales	Líneas oblicuas	Ángulos rectos	Ángulos agudos	Curvas continuas	Curvas discontinuas
A		1	2		3
B	1	3		4			2
C							1
D	1	2		2			1
E	1	3		4
F	1	2		3
G	1	1		1			1
H	2	1		4
I	1	2		4
J	1						1
K	1		2	1	2
L	1	1		1
M	2		2		3
N	2		1		2
O						1
P	1	2		3			1
Q			1		2	1
R	1	2	1	3			1
S							2
T	1	1		2
U	2						1
V			2		1
W			4		3
X			2		2
Y	1		2		1
Z		2	1		2

En realidad, el modelo basado en el análisis de características es semejante al de comparación de plantillas, sólo que aquí las plantillas son las partes geométricas que componen la letra (podríamos llamar a cada característica “miniplantilla”) y en el segundo caso las letras mismas. Parece que este modelo puede explicar lo que el modelo de plantillas puede explicar (ya que las plantillas están compuestas por características) y, además, otra serie de fenómenos para los que el modelo de plantillas es ineficaz.

Volver al índice

VIII. 3. 3. El Pandemonium: base experimental

La teoría del análisis de características (bien sea al modo del Pandemonio, bien sea con otro tipo de architectura) goza de un apoyo experimental razonable, apoyo mayor que la teoría de las plantillas. Veamos alguno de estos experimentos:

En su artículo de 1964 Visual search (“Scientific American”, 210) Neisser planteó la siguiente hipótesis: si el modelo de detección de características es correcto la identificación de una letra (que podríamos llamar letra-objetivo) en un contexto formado por otras letras con características muy semejantes será más lenta que la identificación de una letra en un contexto formado por letras con características muy distintas; por ejemplo la identificación de la letra-objetivo "Z" en el contexto de las letras "X", "L", "N" (letras angulosas) será más lenta que la identificación de dicha letra-objetivo en el contexto de las letras "C", "S" o "G" (letras redondeadas). Esta hipótesis parece razonable puesto que se debe tardar más en rechazar una "N" que una "C", puesto que la "Z" comparte con la "N" más rasgos que con la "C". En los experimentos, los sujetos tardaban más en identificar la letra-objetivo cuando estaban en un contexto con letras similares que cuando estaban en un contexto con letras menos parecidas.
Existen ciertas técnicas que nos permiten preparar el ojo de tal modo que la imagen visual en la retina sea la misma aunque el ojo cambie de posición; en estos casos se observa (y quizá por la fatiga de los receptores retinianos) que la imagen empieza a desaparecer, pero lo hace perdiendo partes significativas, no al azar (la “imagen detenida” va perdiendo líneas rectas, curvas, segmentos significativos, ...). Estos estudios de fragmentación perceptual parecen avalar la teoría del análisis de características.
Otro conjunto de experimentos importante se refiere a las confusiones que se producen en el reconocimiento de letras cuando éstas se presentan en condiciones que dificultan su identificación. Existen varias técnicas para provocar la confusión en los sujetos que realizan la tarea (por ejemplo utilizar el taquistoscopio para presentar estímulos en tiempos extremadamente breves). Los resultados de estos experimentos muestran que las letras que comparten más características tienden a confundirse, algo que la teoría del análisis de características predice.
Algunas investigaciones sugieren la existencia de diversos tipos de células nerviosas funcionalmente distintas, células que responden selectivamente a distintos estímulos: unas a bordes, otras a vértices, otras a barras luminosas, otras a barras oscuras, ...). Sin embargo los resultados y experimentos son controvertidos y no hay un acuerdo unánime en este punto. En el caso de existir la especialización nerviosa citada, la teoría de los detectores de características quedaría fuertemente avalada.

Volver al índice

VIII. 3. 4. El Pandemonium: dificultades

Pero, más allá de su bondad (por ejemplo para explicar la identificación de los caracteres escritos y las formas geométricas sencillas) el modelo del Pandemonium y, en general, la teoría del análisis de características, presenta importantes deficiencias si lo queremos utilizar como una teoría general del reconocimiento de patrones. Veamos alguna de ellas:

El Pandemonium no puede distinguir entre una "T" y una "T" invertida, o una letra y su imagen en el espejo. La causa de estas limitaciones está en el tipo de información que el sistema considera relevante para la identificación: el Pandemonium se fija en los elementos que componen el patrón pero no en sus relaciones estructurales. Las relaciones estructurales tienen que ver, por ejemplo, con el modo de estar localizados y orientados unos rasgos respecto de otros (la simetría, la intersección, la igualdad, ...), y, sin duda, intervienen realmente en el modo en que nosotros reconocemos patrones. Además, posiblemente nuestra mente atiende a este tipo de relaciones para distinguir variantes del mismo patrón: vemos como distintos los signos A, A, A, y A (aunque todos sean ejemplos de la letra "A"), somos capaces de clasificar ejemplos del mismo patrón en grupos a partir de sus semejanzas. Seguramente debido a la limitación citada, el modelo del Pandemonium no puede explicar esta competencia (por ejemplo, el demonio de decisión responderá del mismo modo y sin matices ante dichos signos).

Otra limitación de este modelo es que no introduce datos “de alto nivel” como puede ser la información contextual (se ha demostrado experimentalmente que el sentido global de una frase interviene en la interpretación particular que se le asigna a una letra), o las expectativas inducidas.

Por lo demás, cuando creamos un Pandemonium e intentamos comprobar su validez, parece necesario que nosotros hayamos interpretado antes el estímulo en los términos de las categorías físicas que el propio sistema utiliza para definir el patrón (líneas rectas, curvas, ángulos, ...), de tal manera que, en realidad, el Pandemonium interpreta lo que antes nosotros hemos interpretado del estímulo, no interpreta el estímulo mismo; para que de verdad fuese capaz de realizar esto último al sistema se le debería presentar la energía luminosa del propio estímulo (es decir, debería estar conectado a un sensor y utilizar los datos que éste le ofrezca). Por ejemplo, si al sistema le presentamos una letra que conste de una línea recta, no es cierto que el estímulo básico o primitivo sea propiamente una línea recta pues esto ya exige una interpretación (es necesario saber qué es una línea recta); nuestra mente es capaz de descubrir líneas rectas en el entorno, y es necesario una explicación de esta competencia; el Pandemonium no da cuenta de la habilidad de nuestra mente para captar este tipo de regularidad en los estímulos. O dicho en otros términos: en el reconocimiento de patrones existe un procesamiento de la información anterior y más básico que el que nos ofrece los modelos al estilo del Pandemonium.

Por último, y relacionado con lo anterior, el modelo del Pandemonium tiene poca validez ecológica: puede ser competente en situaciones bastante artificiales (pocos patrones, cada uno de ellos compuesto de un número reducido de categorías y que se ofrecen en condiciones perceptuales óptimas), como ocurre en el caso de las letras del alfabeto; sin embargo, en situaciones normales, los estímulos son objetos tridimensionales y se ofrecen en condiciones físicas no necesariamente perfectas (poca iluminación, sombras, escorzos, mezcla de unos objetos con otros, ...); en estas situaciones reales la eficacia de un Pandemonium es prácticamente nula.

Volver al índice

VIII. 3. 5. El Pandemonium y el conexionismo

Este modelo de identificación de patrones se puede incluir en el enfoque conexionista pues presenta algunos de sus rasgos principales:

1. Existen muchas unidades de procesamiento.

2. La información se almacena de un modo bastante distribuido: en el nivel de los demonios de características cada letra se define por la activación de un conjunto de unidades y cada unidad colabora en la identificación de varias letras.

3. El procesamiento es en paralelo pues todas las unidades de cada nivel actúan simultáneamente.

4. Las unidades están conectadas entre sí formando distintos niveles o capas.

5. La entrada y la salida de cada una de las unidades se expresa de modo cuantitativo.

6. El cómputo que realiza el sistema es básicamente de tipo cuantitativo y probabilístico (los demonios cognitivos reciben información cuantitativa de los demonios de características y envían su señal al demonio de decisión de modo cuantitativo (gritando mucho, poco o nada).

Pero también encontramos algunas importantes diferencias:

La primera y más llamativa se refiere al sistema de representación gráfica utilizado: en los modelos conexionistas típicos las unidades se suelen representar con círculos, reciben el nombre de neuronas y las conexiones entre ellas se representan mediante líneas rectas; en el Pandemonium las unidades reciben el nombre de demonios, se las representa mediante pequeños diablillos, y las conexiones entre ellas mediante flechas más o menos imaginativas.
En el Pandemonium las conexiones son excitatorias: en el sentido de que si un demonio de características detecta un característica envía su señal a un demonio cognitivo provocando un aumento en la posibilidad de que este se active o un incremento en su activación; a su vez el incremento de los demonios cognitivos provoca un aumento en la posibilidad de que el demonio de decisión se decida por el carácter que representa dicho demonio cognitivo; pero el Pandemonium (al menos en sus versiones más sencillas) no presenta conexiones inhibitorias mientras que las redes conexionistas tradicionales sí lo hacen.
Aunque, como se ha dicho, el sistema es un sistema de representación distribuida, las redes tradicionales distribuyen de un modo más acentuado la información. Un aspecto de esta diferencia se refiere a la interpretación cognitiva: en los modelos de redes conexionistas en los que la información está más distribuida las unidades no representan ni significan nada, los significados y las representaciones aparecen como consecuencia de la interacción entre una muchedumbre de unidades, y se reflejan particularmente en el patrón de pesos y el patrón de actividad. En el Pandemonium hay, al menos, un nivel en el que es posible la interpretación cognitiva puesto que en él la información se representa de forma localista y no distribuida (el de los demonios de características, en donde cada demonio representa una letra) Por otro lado, es cierto que también se han propuesto importantes ejemplos de redes conexionistas con unidades que permiten una interpretación cognitiva (por ejemplo la red NETtalk explicada más abajo), y, por lo tanto, representaciones locales.
El Pandemonium no presenta de modo preciso las modificaciones cuantitativas que sufren las unidades (por ejemplo la intensidad exacta necesaria para la activación de un demonio cognitivo, ni la magnitud exacta de la señal que envía un demonio cognitivo al demonio de decisión para que se decida por la letra correspondiente al demonio cognitivo).
En el modelo tampoco encontramos conceptos habituales en el procesamiento de las redes conexionistas tradicionales (umbral, función de activación, función de transferencia, .... );
El procesamiento realizado por el Pandemonium depende de las asignaciones que el diseñador del sistema a establecido, las cuales dependen, a su vez, de la comprensión que el diseñador tiene de las características esenciales de las letras (por ejemplo, considerar que la características esenciales de la letra G son tener una línea vertical, una línea horizontal, un ángulo recto y una curva discontinua); por esta razón en realidad el Pandemonium no es un sistema capaz de aprender a reconocer formas (no sufre un proceso de modificación de las unidades para adecuar la entrada con la salida del sistema) ni utiliza algoritmos de aprendizaje; sin embargo las redes tradicionales pueden aprender en el sentido citado y para ello disponen de algoritmos de aprendizaje. El Pandemonium puede llegar a reconocer patrones pero su capacidad se debe básicamente a la comprensión que el diseñador tiene de la estructura de los patrones que ha de identificar.

De todos modos, las diferencias anteriores no son significativas pues algunas se refieren incluso a cuestiones de índole estético (el uso de “demonio” en vez de “neurona”, o los dibujos de las unidades); y la mayoría de ellos se deben a la falta de concreción con habitualmente se presenta el Pandemonium. De hecho es posible utilizar las ideas básicas que utiliza este modelo para explicar nuestra capacidad para reconocer patrones y reflejarla de un modo más preciso y detallado y en términos similares a las redes conexionistas tradicionales. Es lo que ocurriría si intentásemos implementar el Pandemonium en un ordenador; en este caso sería preciso concretar con precisión las modificaciones cuantitativas que afectan a las unidades, a la vez que las funciones matemáticas que determinan el cómputo en los distintos niveles de procesamiento; incluso podrían añadirse conexiones inhibitorias para favorecer el procesamiento. Con estos complementos (que no implican un cambio en el modelo sino su concreción) la representación y arquitectura del Pandemonium de Selfridge tendría el mismo aroma que los modelos conexionistas tradicionales.

Sin embargo, en donde las diferencias están más marcadas es en el tema del aprendizaje. Ya se ha dicho que una de las características principales de las redes conexionistas es que aprenden a reconocer patrones, no sólo que reconocen patrones; pero en el caso del Pandemonium quien debe aprender es el diseñador de la red: debe descubrir y aprender cuáles son las características básicas que tiene cada letra (ángulos, líneas rectas, líneas curvas, ...) y debe descubrir “a mano” las dificultades con las que puede tropezar el sistema para realizar un procesamiento eficaz. Por ejemplo, si intentamos poner en funcionamiento el Pandemonium podemos observar que en principio tendría dificultades para distinguir la letra "P" de la "R": la "P" tiene una línea vertical, dos horizontales, tres ángulos rectos y una curva discontinua y la "R" todas ellas más una línea oblicua, de modo que los demonios cognitivos de la "P" y la "R" se activan por igual y el demonio de decisión no podrá elegir entre ellos. El diseñador ha de utilizar alguna estrategia para resolver este problema, por ejemplo obligar a que un demonio cognitivo se active al máximo si y sólo si están presentes todas las características de la letra correspondiente, de este modo tanto la ausencia de una característica como la presencia de una característica irrelevante inhibirá la respuesta de la unidad. Con este ejemplo se quiere señalar que el modelo del Pandemonium exige que el diseñador conozca la “lógica” del procesamiento de la información para el reconocimiento de patrones, algo que, como se sabe, constituye uno de los objetivos de la psicología cognitiva tradicional. Esto no ocurre en el caso de los modelos conexionistas: en ellos la red utiliza algoritmos para la modificación de los pesos de sus conexiones y gracias a dichas modificaciones puede aprender por sí misma a reconocer los patrones (una consecuencia de ello es que en los modelos conexionistas no es posible saber cuáles son los elementos relevantes que la red toma en cuenta para el procesamiento ni el orden ni la lógica de dicho procesamiento; precisamente la originalidad del planteamiento conexionista es que rechaza la existencia de reglas de procesamiento).

Volver al índice

VIII. 4. NETtalk: aprender a leer en inglés

Terrence Sejnowsky y Charles R. Rosenberg escribieron en 1986 NETtalk: A Parallel Network that Learns to Read Aloud. En este artículo presentaron la red NETtalk, cuya finalidad era leer y hablar textos en inglés.

NETtalk tiene una estructura de tres capas interconectadas con cerca de 20.000 sinapsis:

en la capa de entrada encontramos 7 grupos de 29 unidades cada uno (203 unidades de entrada);
la capa oculta consta de 80 unidades;
y la capa de salida de 26 unidades.

De las 29 neuronas que consta cada grupo de la capa sensorial, 26 codifican una letra del alfabeto inglés y las otras tres restantes la puntuación y los límites entre palabras. Puesto que las unidades de entrada se distribuyen en siete grupos, el patrón de entrada que la red es capaz de reconocer ha de ser de 7 caracteres como máximo. Las unidades de salida o motoras codifican las dimensiones fundamentales del habla: fonemas, acentos y hiatos entre sílabas.

La red transformaba los datos de entrada (las letras) en fonemas o sonidos. Dado que los pesos originales se establecieron al azar, los primeros resultados no eran buenos; el entrenamiento consistió en presentar cerca de 1000 palabras del habla corriente de un niño; un “maestro” o supervisor controlaba la corrección de la respuesta de la red y modificaba los pesos mediante la regla delta generalizada (entrenamiento con propagación hacia atrás). Tras casi 50.000 presentaciones y las modificaciones correspondientes de sus pesos, la red era capaz de leer y hablar con una exactitud del 95 por ciento.

Resultan sorprendentes algunas semejanzas entre NETtalk y la capacidad lingüística humana:

la progresiva eficacia de la red guarda cierta semejanza con la de los niños: las primeras respuestas se parecen a los balbuceos sin sentido de un bebé, pero el sucesivo ajuste de los pesos mejora la calidad de los balbuceos lentamente, hasta culminar en unas respuestas coherentes e inteligibles ante cualquier texto en inglés;
es capaz de generalizar: al presentarle nuevas palabras del mismo niño el sistema era capaz de leer y pronunciar con una exactitud del 78 por ciento;
degradación elegante: la red muestra una clara resistencia al daño; la destrucción de algunos elementos de la red no tiene consecuencias catastróficas en el rendimiento total, simplemente disminuye su rendimiento.

Las propiedades citadas son las que cabría esperar de un sistema de procesamiento distribuido y paralelo (como se ha comentado en la sección correspondiente), y, sin duda, resulta más eficaz para modelar la capacidad humana para detectar patrones que los modelos de plantillas y de análisis de características.

La figura siguiente es un esquema simplificado de la arquitectura del NETtalk (tomado de Soledad Ballesteros, Psicología General. Un enfoque cognitivo).

Volver al índice

CONEXIONISMO VIII. Algunos modelos de redes neuronales

CONEXIONISMO

VIII. Algunos modelos de redes neuronales